Enhancing the Performance of Graph Algorithms — Part 2

Introduction to the Heaps, Their Implementations, and Time Complexity Analysis

We have seen about the Graph Algorithms and have already discussed their Time Complexity in our previous article “Enhancing the Performance of Graph Algorithms — Part 1”.

Heaps

A heap is a type of tree-based data structure that fulfills the heap property.

Heap Property: If Q is a child node of P, then key(P) ≥ key (Q). As a result, an element with the greatest key is always in the root node, and such a heap is sometimes referred to as a max-heap.

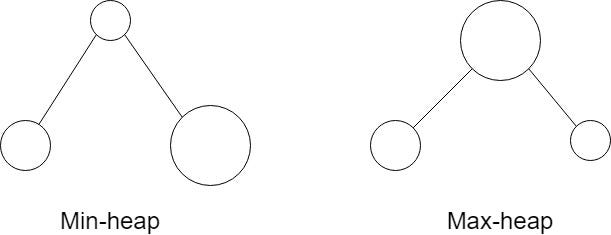
There is, of course, a min-heap. For a min-heap, the parent node will always lesser than the child nodes. The root node will have the lowest element.

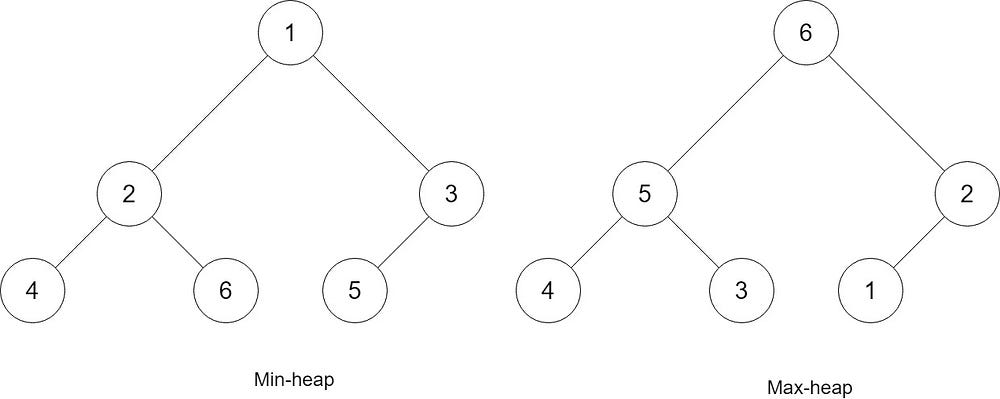
Let’s see how a min-heap is working

As in the definition, the min-heap has to follow the heap property. That is if Q is a child node of P, then key(P) ≤ key (Q).

The heap can also be stored in an array, which is a more common approach. Because heap is always a complete binary tree, it can be stored in a small amount of space. Pointers take up no space; instead, the parent and children of each node can be found using simple arithmetic on array indices.

The rules (assume the root is stored in arr[0]). For each index i, element arr[i] has children at arr[2i + 1] and arr[2i + 2], and the parent at arr[floor( ( i — 1 )/2 )].

This implementation is especially useful in the heapsort algorithm, as it allows the space in the input array to be reused for heap storage (i.e., the algorithm is in place). However, it necessitates allocating the array before filling it, making this method unsuitable for implementing priority queues where the number of elements is unknown.

It is completely acceptable to implement a binary heap using a traditional binary tree data structure. When adding an element, there is a problem finding the adjacent element on the last level of the binary heap.

Insertion of elements in a min-heap

Let’s add 100 as the 1st element into an empty heap.

Let’s add 50 as the 2nd element.

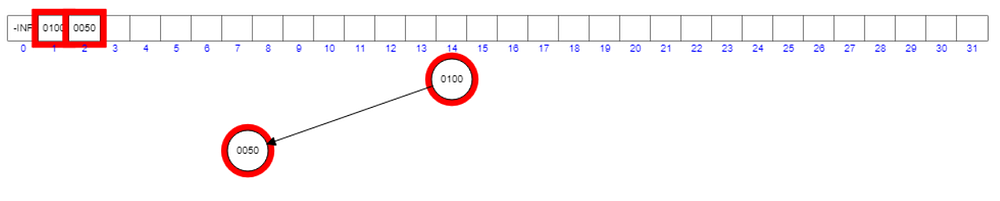
Here you can see 50 is lesser than 100 and 100 is in parent node to the 50. This violates the heap property of min-heap. So we have to exchange the positions of 50 and 100.

Let’s add 80 now.

Since 80 is greater than 50, there won’t be any changes in the node. Note that, 80 is lesser than 100 but it didn’t go to the next level and got interchanged with 100. because it is a complete binary tree. Let’s add 40 now.

A new violation to the heap property. What should we do now? Interchange 100 and 40.

Still, we have a problem. Interchange 50 and 40.

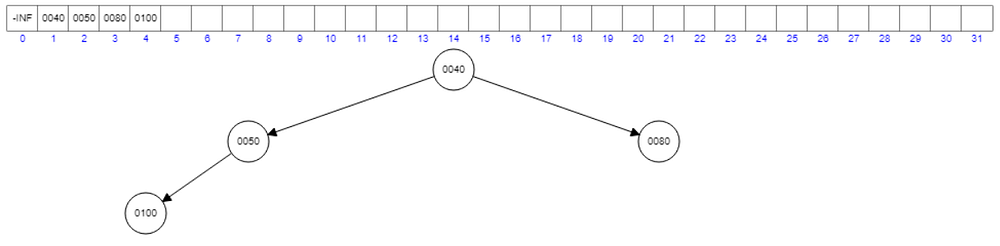
Let’s add 70, 90, and 120.

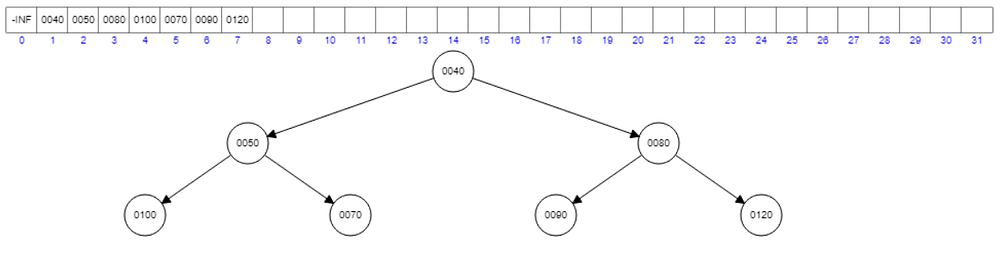
Now, let’s add 30.

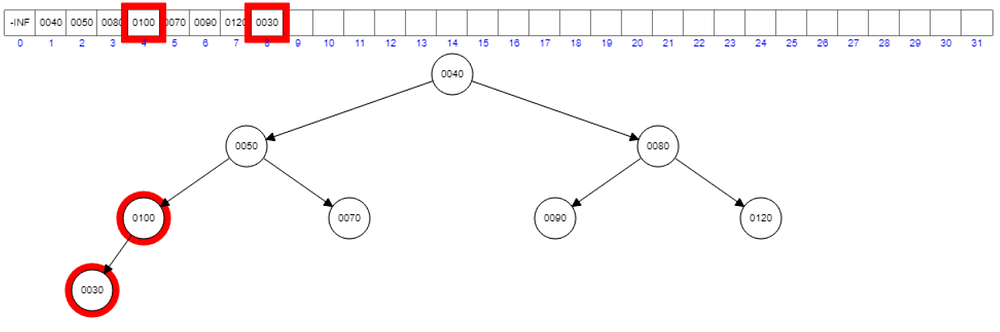
Violation to the property. Interchange 100 and 30. Then we will have another violation with 50.

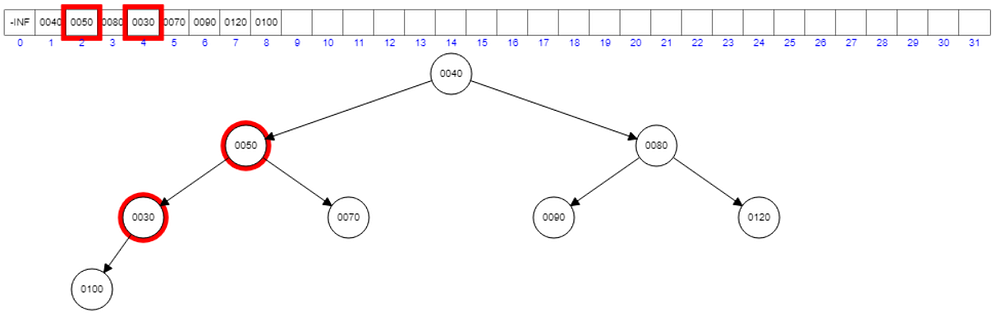
Interchange 50 with 30. Then we will have another violation with the root node 40.

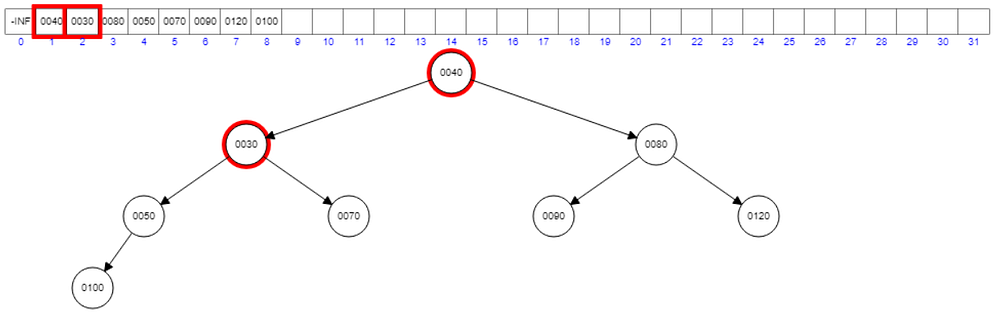
Interchange 40 with 30 and now the new root node will be 30.

The insertion works like this.

1. First and foremost, always insert at the bottom of the tree. The inserted element’s initial position is at the bottom level.
2. We must now update the position of this element in order to satisfy the min-heap property.
3. Check the sub-tree of its immediate parent because the root node of every sub-tree must be the smallest.
4. If the parent is greater than this inserted element, we must swap it to update its position.
5. But we’re not done yet, because the updated node’s sub-min-heap tree’s property may be violated!
6. We must continue swapping until we reach the root node, at which point we are finished.

Deletion of elements in a min-heap

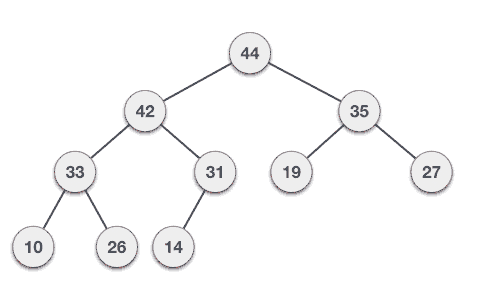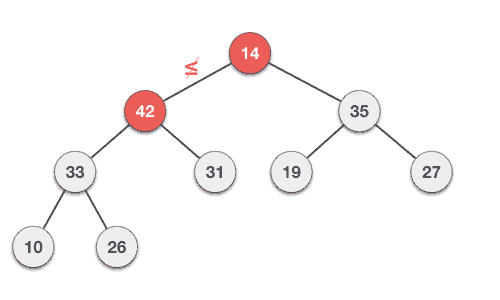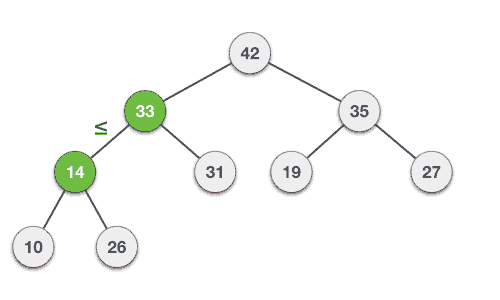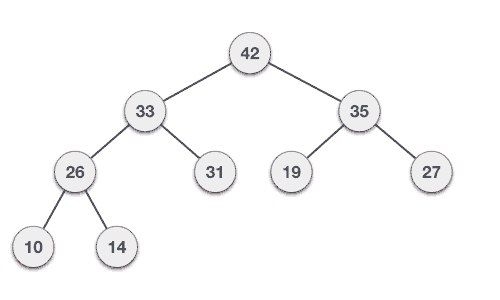
In the min-heap we made above, let’s remove the root element.

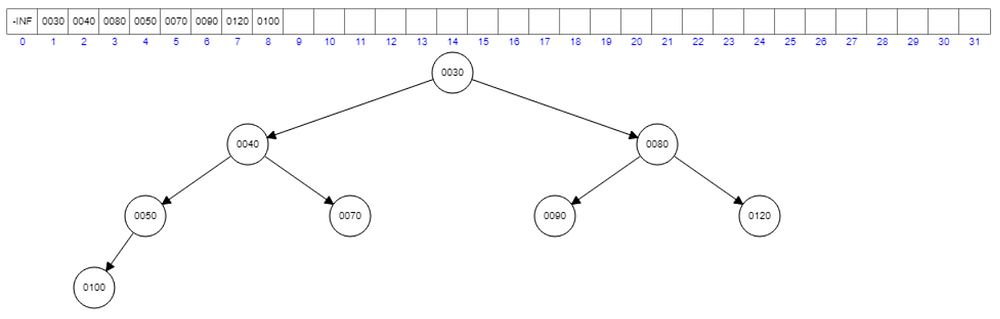
The root is 30. When we remove the root, the last element, that is; 100 will take the position of the root. Now we have a violation of heap property. To know which to replace 100, we have to compare both children 40 and 80.

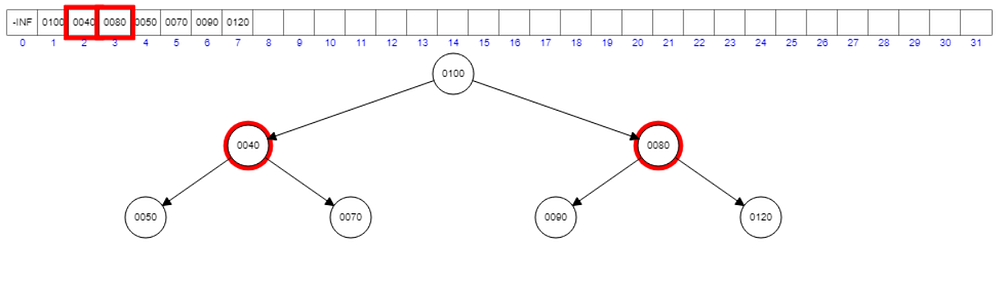
Since 40 < 80, we can interchange 100 with 40.

There we will have another violation like this.

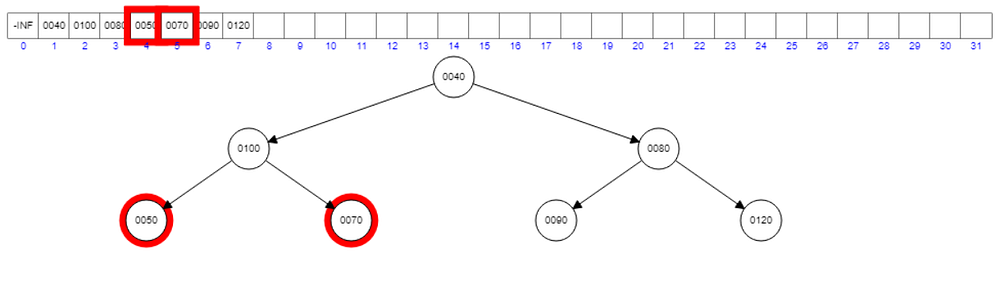
100 > 70, 50

So we need to interchange the parent with one of these two, 70 and 50. As we did earlier, we have to find the minimum from 70 and 50, and then we can interchange 100 with that minimum value.

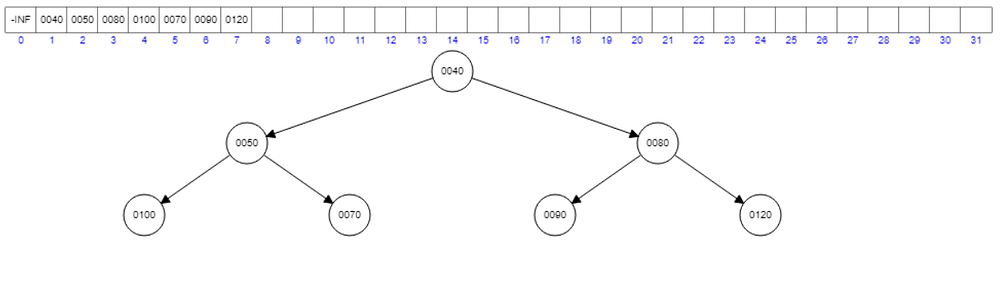
Now we have this. See the root element, it is now having 40 which is the lowest in all available values.

What will happen if we remove the root once again?

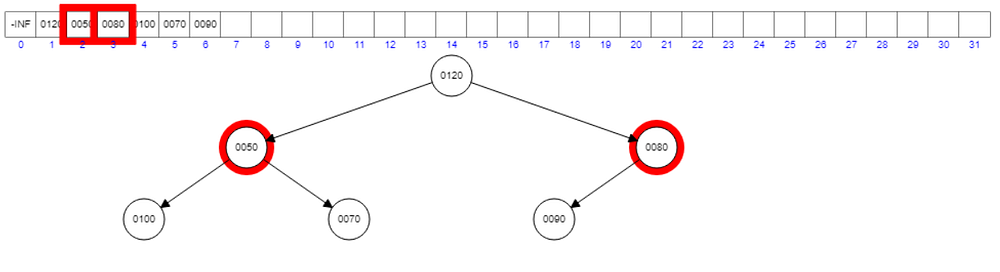
120 will take the root place and that will create a violation to the heap property.

The interchange of the location of 120 and 50 will result in another violation like this. And therefore we have to interchange the minimum between 100 and 70 with 120. The result will be like this.

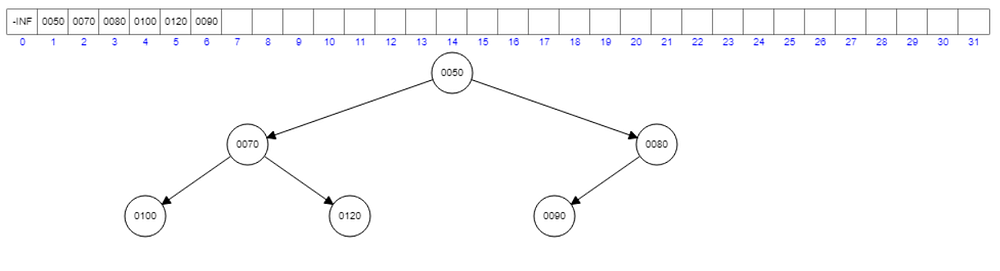
Deletion works like this.

1. Update the root with the last element.
2. The last element at the bottom will now be removed. In the end, this is similar to swapping and deleting! Only because we no longer care about the root value do we simply update it.
3. The issue here is that we need to keep the min-heap property.
4. As a result, we must ensure that the entire tree retains this property. To accomplish this, we will use a function called heapify().

The heapify() procedure

1. This function accepts an element index and keeps the min-heap property by exchanging with the smallest element in its immediate sub-tree.
2. The tree that results will satisfy the min-heap property.
3. This entails locating the sub-minimum tree’s element and swapping it with the current element.
4. Following that, we must ensure that the entire tree meets this requirement. As a result, we must recursively invoke the procedure on the smallest element until we reach the root!

Time Complexity of Implementation

1. Getting the minimum O(1)
2. Insertion and deletion O(logN)
3. Heapify O(logN)

Max-heaps

Similar to min-heap but with the opposite property.

Insertion of elements

Deletion of elements

How can we make use of this Data Structure in Algorithms on Graphs?

The most famous solution for finding the shortest path was first proposed by Dijkstra. Generally, his solution is the most efficient and used in most cases. On average each of N nodes is processed, and for each, all of its neighbors are updated in O(N). Thus the complexity is O(N²).

This complexity can be optimized by using a min-heap. But How?

A complexity of O(NlogN) can be obtained for sparse graphs. A heap is used to store the shortest distances between nodes, and lists are used to store the neighbors of each node. In this manner, the unprocessed node with the shortest distance is found in logN, so each node is updated in logN as well.

Given a sparse graph, each node has few neighbors, and thus the average complexity is O(NlogN).

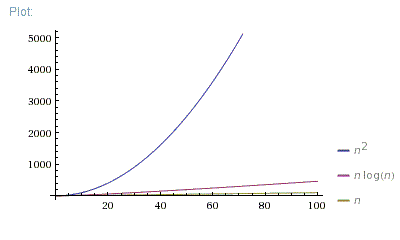
Which is better? N² or NlogN?

    N log(N)
lim --------- = 0 where N goes to infinity
       N²

Proof:

     N log(N)        log(N)   
lim --------- = lim -------- = 
       N²              N

(Applying L Hopital law)
        1/N          1
= lim ------- = lim --- = 0
         1           N

That means N² grows faster, so Nlog(N) is smaller (better) when N is high enough.

Try to implement this in the Astar algorithm as well and compare the execution time when you use Priority Queues. Play with this amazing Data Structure by implementing it in Algorithms on graphs.

Hope this can help. Share your thoughts too.